CBSE Class 10 Maths Basic 2025 430/1/1 Set 1
If the HCF of two positive integers \(a\) and \(b\) is 1, then their LCM is:
Step 1: Recall the Key Relationship
For any two positive integers a and b:
\( \text{HCF}(a, b) \times \text{LCM}(a, b)\) \(= a \times b \)
Step 2: Substitute Given HCF
Here, it's given that \( \text{HCF}(a, b) = 1 \)
\(\Rightarrow 1 \times \text{LCM}(a, b) = a \times b \)
Step 3: Solve for LCM
So,
\( \text{LCM}(a, b) = a \times b \)
Step 4: Final Answer
When two positive integers have HCF 1 (they are co-prime), their Least Common Multiple is simply their product: \( ab \) (option D).
The number \(3 + \sqrt{2}\) is:
Step 1: Identify the Types of Numbers
The number 3 is a rational number because it can be expressed as a fraction \(\displaystyle \frac{3}{1} \).
Step 2: Understand the Nature of \(\sqrt{2}\)
The number \( \sqrt{2} \) is known to be an irrational number because it cannot be expressed as a simple fraction.
Step 3: Sum of Rational and Irrational
The sum of a rational number \((3)\) and an irrational number \((\sqrt{2})\) is always an irrational number.
Step 4: Final Answer
Therefore, \(3 + \sqrt{2}\) is an irrational number (option B).
The discriminant of the quadratic equation \(x^2 - 3x - 2 = 0\) is:
Step 1: Identify the quadratic equation coefficients
The given quadratic equation is \(x^2 - 3x - 2 = 0\). Here, \(a = 1\), \(b = -3\), and \(c = -2\).
Step 2: Recall the discriminant formula
The discriminant \(D\) of a quadratic equation \(ax^2 + bx + c = 0\) is given by:
\( D = b^2 - 4ac \)
Step 3: Substitute the values
Substitute \(a = 1\), \(b = -3\), and \(c = -2\) into the formula:
\( D = (-3)^2 - 4 \times 1 \times (-2)\) \(= 9 + 8 = 17 \)
Step 4: Final Answer
The discriminant of the quadratic equation is \( 17 \) (option B).
The equation \( x + \displaystyle\frac{1}{x} = 3 \ (x\ne0) \) is expressed as a quadratic equation in the form of \( ax^2 + bx + c = 0 \). The value of \( a - b + c \) is:
Step 1: Given Equation
The equation is \(\displaystyle x + \frac{1}{x} = 3 \) where \( x \ne 0 \).
Step 2: Convert to Quadratic Form
Multiply both sides by \( x \) to eliminate the fraction:
\(\displaystyle x \times x + x \times \frac{1}{x} = 3 \times x \)
\(\Rightarrow x^2 + 1 = 3x \)
Step 3: Rearrange to Standard Quadratic Format
Bring all terms to one side:
\( x^2 - 3x + 1 = 0 \)
Step 4: Identify coefficients and calculate \( a - b + c \)
Here, \( a = 1 \), \( b = -3 \), and \( c = 1 \).
Calculate: \( a - b + c \) \(= 1 - (-3) + 1\) \(= 1 + 3 + 1 \) \(= 5 \)
Step 5: Final Answer:
The value of \( a - b + c \) is 5 (Option A).
For the point \((3, -5)\), the value of (abscissa - ordinate) is:
Step 1: Understand the terms
The abscissa of a point is the x-coordinate, and the ordinate is the y-coordinate.
Step 2: Identify coordinates
Given the point is \((3, -5)\), so:
Abscissa (x) = 3
Ordinate (y) = -5
Step 3: Calculate (abscissa - ordinate)
\( 3 - (-5) = 3 + 5 = 8 \)
Step 4: Final Answer:
The value of (abscissa - ordinate) is 8 (Option D).
The mid-point of a line segment divides the line segment in the ratio:
Step 1: Understand the concept of midpoint
The midpoint of a line segment is the point that divides the segment into two equal parts.
Step 2: Ratio of division
Since the midpoint divides the segment into two equal parts, the ratio is:
\( 1 : 1 \)
Step 3: Final Answer:
The midpoint divides the line segment in the ratio 1 : 1 (Option C).
Which of the following is not a criterion for similarity of triangles?
Step 1: Understand criteria for similarity of triangles
The common criteria for triangle similarity are:
- AAA (Angle-Angle-Angle): If all corresponding angles are equal, triangles are similar.
- SSS (Side-Side-Side): If all three corresponding sides are in proportion, triangles are similar.
- SAS (Side-Angle-Side): If two sides are in proportion and the included angle is equal, triangles are similar.
Step 2: Identify the option that is not a similarity criterion
RHS (Right angle-Hypotenuse-Side) is a criterion for congruence of right-angled triangles, not for similarity.
Step 3:Final Answer:
Option D (RHS) is not a criterion for similarity of triangles.
From the figures given below, which of the following is true about the measure of \(∠\; \text {P }\)?
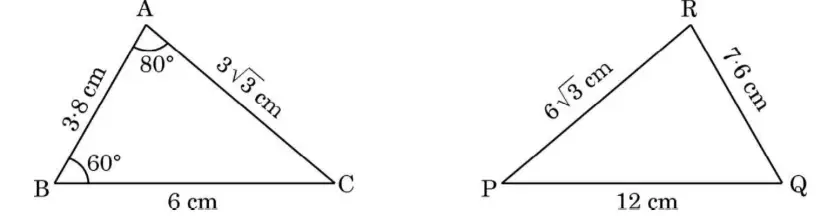
Step 1: Check similarity between the triangles
Triangle ABC and triangle RQP have sides in proportion (each side of RQP is 2 times the corresponding side of ABC: AB = 3.8, RQ = 7.6; BC = 6, QP = 12; AC = \(3\sqrt{3}\), RP = \(6\sqrt{3}\)), so they are similar triangles (SSS similarity criterion).
Step 2: Match corresponding angles
In similar triangles, corresponding angles are equal. Let’s match angles by position:
In triangle ABC, angle at A = 80°, B = 60°, C = 40°.
Sides opposite these angles:
- AB (opposite C) → RQ (opposite P)
- BC (opposite A) → QP (opposite R)
- AC (opposite B) → RP (opposite Q)
Step 3: Final Answer:
Therefore, the measure of \( \angle \text P \) is \(40^\circ\) Option C .
In the given figure, PA is a tangent to a circle with centre O. If \( \text {OP} = 10\,\text{cm} \), then the length of AP is:
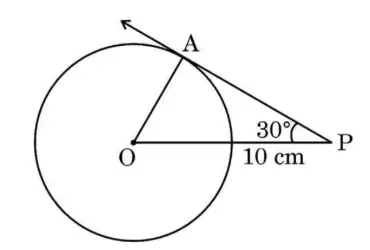
Step 1: Understand the triangle OAP
Triangle OAP has:
• ∠OAP = 90° (right angle at point of tangency)
• ∠OPA = 30°
• OP = 10 cm (hypotenuse)
Step 2: Use the right triangle ratios
OA is opposite to angle ∠OPA (30°); AP is adjacent.
By trigonometry:
\( \sin(30^\circ) \) \(\displaystyle= \frac{\text{Opposite}}{\text{Hypotenuse}} \) \(\displaystyle= \frac{\text{OA}}{10} \)
\(\displaystyle \sin(30^\circ) = \frac{1}{2} \)
So, \( \displaystyle \frac{1}{2} = \frac{\text{OA}}{10}\)
\( \Rightarrow \text{OA} = 5 \) cm (radius).
Step 3: Find AP using cosine
\(\displaystyle \cos(30^\circ) = \frac{\text{Adjacent}}{\text{Hypotenuse}}\) \( = \frac{\text{AP}}{10} \)
\( \displaystyle \cos(30^\circ) = \frac{\sqrt{3}}{2} \)
So, \(
\displaystyle\frac{\sqrt{3}}{2} = \frac{\text{AP}}{10}\)
\(\Rightarrow \text{AP}\displaystyle = 10 \times \frac{\sqrt{3}}{2} \) \(= 5\sqrt{3} \) cm.
Final Answer: The length of AP is 5\(\sqrt{3}\) cm (Option D).
Which of the following statements is false?
Step 1: Evaluate each given trigonometric statement
- \(\tan 45^\circ = \cot 45^\circ\)
Both \(\tan 45^\circ\) and \(\cot 45^\circ\) equal 1, so this is true. - \(\sin 90^\circ = \tan 45^\circ\)
\(\sin 90^\circ = 1\), \(\tan 45^\circ = 1\), so this is true. - \(\sin 30^\circ = \cos 30^\circ\)
\(\sin 30^\circ = \frac{1}{2}\), \(\displaystyle\cos 30^\circ = \frac{\sqrt{3}}{2} \approx 0.866\), so this is false. - \(\sin 45^\circ = \cos 45^\circ\)
Both equal \(\displaystyle \frac{\sqrt{2}}{2} \approx 0.707\), so this is true.
Step 2: Identify the false statement
The false statement is Option C: \(\sin 30^\circ = \cos 30^\circ\).
Final Answer: Option C is false.
The value of \(\left(\tan^2 \text A - \displaystyle \frac{1}{\cos^2 \text A}\right)\) is:
Step 1: Express the given expression
The expression is:
\(\displaystyle
\tan^2 A - \frac{1}{\cos^2 A}
\)
Step 2: Use trigonometric identities
Recall that \(\displaystyle \tan A = \frac{\sin A}{\cos A}\), so
\(\displaystyle
\tan^2 A = \frac{\sin^2 A}{\cos^2 A}
\)
Substitute this into the expression:
\(\displaystyle
\frac{\sin^2 A}{\cos^2 A} - \frac{1}{\cos^2 A}\) \( \displaystyle = \frac{\sin^2 A - 1}{\cos^2 A}
\)
Step 3: Simplify numerator using Pythagorean identity
Recall that \(\sin^2 A + \cos^2 A = 1\), so
\(
\sin^2 A - 1 = -\cos^2 A
\)
Substitute:
\(\displaystyle
\frac{-\cos^2 A}{\cos^2 A} = -1
\)
Final Answer: The value of the expression is \(-1\) (Option D).
In the given figure, which of the following angles represents the angle of depression?
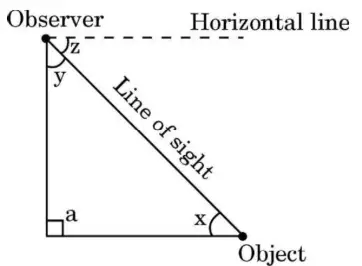
Step 1: Understand the angle of depression
The angle of depression is formed between the horizontal line from the observer's eye and the line of sight down to the object.
Step 2: Locate the angle in the diagram
In the figure, the angle marked z is between the horizontal line (from observer) and the line of sight, which matches the definition of the angle of depression.
Final Answer: The angle that represents the angle of depression is z (Option C).
The perimeter of the shaded region in the given figure is :
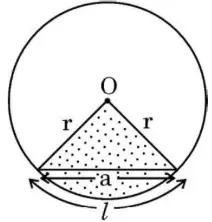
Step 1: Analyze the shaded region
The shaded region is a triangle within a circle, with two sides equal to the radius \(r\) and the curved part at the base (arc length) denoted by \(l\).
Step 2: Find the perimeter
The perimeter of the shaded region consists of the two radii (\(r + r = 2r\)) and the arc length (\(l\)). The segment denoted as "a" is inside the triangle, not on the boundary of the shaded region.
Final Answer: The perimeter is \(l + 2r\) (Option C).
The ratio of the area of a quadrant of a circle to the area of the same circle is :
Step 1: Find the area of a circle
The area of a circle is \( \pi r^2 \).
Step 2: Find the area of a quadrant
A quadrant is one-fourth of a circle, so its area is \( \frac{1}{4} \pi r^2 \).
Step 3: Calculate the ratio
Ratio = (area of quadrant) : (area of whole circle) = \( \frac{1}{4} \pi r^2 : \pi r^2 = 1 : 4 \)
Final Answer: The ratio is 1 : 4 (Option C).
For which of the following solids is the lateral/curved surface area and total surface area the same?
Step 1: Definitions
The total surface area is the sum of all the areas that cover the outside of a solid.
The lateral/curved surface area is the area of only the sides, without the top and bottom faces (if any).
Step 2: Sphere uniqueness
For a sphere, there are no distinct faces or bases - its entire outer surface is curved. So, the lateral/curved surface area and total surface area are both \(4\pi r^2\).
Final Answer: The solid for which lateral/curved surface area and total surface area are the same is the sphere (Option D).
The class mark of the median class of the following data is :
| Class Interval | 10 – 25 | 25 – 40 | 40 – 55 | 55 – 70 | 70 – 85 | 85 – 100 |
|---|---|---|---|---|---|---|
| Frequency | 2 | 3 | 7 | 6 | 6 | 6 |
Step 1: Calculate the total frequency
Add all the frequencies given:
\( 2 + 3 + 7 + 6 + 6 + 6 = 30 \)
The total number of observations, \( n = 30 \).
Step 2: Find the median class
The median class is the class interval where the cumulative frequency is equal to or just exceeds half of the total frequency.
Half of total frequency \(= \displaystyle \frac{30}{2} = 15 \).
Calculate cumulative frequencies:
- \(10-25: 2\)
- \(25-40: 2 + 3 = 5\)
- \(40-55: 5 + 7 = 12\)
- \(55-70: 12 + 6 = 18\) → This is the first cumulative frequency greater than or equal to 15.
Therefore, the median class is \( 55 - 70 \).
Step 3: Calculate the class mark of the median class
The class mark is the midpoint of the class interval:
\( \displaystyle \text{Class mark} = \frac{55 + 70}{2} = 62.5 \)
Final Answer: The class mark of the median class is 62.5 (Option D).
The following distribution shows the number of runs scored by some batsmen in test matches :
| Runs Scored | 3000 – 4000 | 4000 – 5000 | 5000 – 6000 | 6000 – 7000 |
|---|---|---|---|---|
| Number of Batsmen | 5 | 10 | 9 | 8 |
The lower limit of the modal class is :
Step 1: Understand what modal class means
The modal class is the class interval in a grouped frequency distribution which has the highest frequency.
It represents the interval where the data is most concentrated or common.
Step 2: Look at the frequency values
From the table, the frequencies (number of batsmen) for each class are:
- 3000 – 4000: 5
- 4000 – 5000: 10
- 5000 – 6000: 9
- 6000 – 7000: 8
The highest frequency is 10, which belongs to the class 4000 – 5000.
Step 3: Identify the lower limit of the modal class
Since the modal class is 4000 – 5000, its lower limit is 4000.
Final Answer: The lower limit of the modal class is 4000 (Option B).
In a random experiment of throwing a die, which of the following is a sure event?
Step 1: Understand the concept of a sure event
A sure event is an event that is certain to happen when an experiment is performed. Its probability is 1.
Step 2: Analyze the outcomes of throwing a die
A die has 6 faces numbered from 1 to 6.
Possible outcomes are: 1, 2, 3, 4, 5, 6.
Step 3: Evaluate each option
- Option A: Getting a number between 1 and 6 – This is true for every throw (all outcomes), so this is a sure event.
- Option B: Getting an odd number < 7 – Possible odd numbers are 1, 3, 5. Not all outcomes are odd, so this is not a sure event.
- Option C: Getting an even number < 7 – Possible even numbers are 2, 4, 6. Not all outcomes are even, so this is not a sure event.
- Option D: Getting a natural number < 7 – Natural numbers less than 7 are 1, 2, 3, 4, 5, 6. This includes all possible outcomes, so this is a sure event.
Final Answer: The sure event is Getting a natural number < 7 (Option D).
Assertion (A): For any two natural numbers a and b, the HCF of a and b is a factor of the LCM of a and b.
Reason (R): HCF of any two natural numbers divides both the numbers.
Step 1: Understand the assertion
Assertion (A) states that for any two natural numbers \(a\) and \(b\), the HCF (Highest Common Factor) of \(a\) and \(b\) is a factor of their LCM (Least Common Multiple).
Step 2: Understand the reason
Reason (R) states that the HCF of two natural numbers divides both numbers.
Step 3: Verify the assertion through example
Take \(a = 12\) and \(b = 18\) as example numbers.
- Factors of 12 are \(1, 2, 3, 4, 6, 12\).
- Factors of 18 are \(1, 2, 3, 6, 9, 18\).
- Common factors are \(1, 2, 3, 6\), so \(\text{HCF}(12, 18) = 6\).
Step 4: Calculate the LCM
- Multiples of 12 are \(12, 24, 36, 48, 60, 72, \ldots\).
- Multiples of 18 are \(18, 36, 54, 72, \ldots\).
- The smallest common multiple is \(36\), so \(\text{LCM}(12, 18) = 36\).
Step 5: Verify the relation between HCF, LCM, and the numbers
- Compute \(\text{HCF} \times \text{LCM} \) \(= 6 \times 36 = 216\).
- Compute \(a \times b = 12 \times 18 = 216\).
This confirms the formula \(a \times b \) \(= \text{HCF}(a, b) \times \text{LCM}(a, b)\) holds.
Step 6: Check if HCF divides LCM
- Calculate \(\displaystyle \frac{\text{LCM}}{\text{HCF}} = \displaystyle \frac{36}{6} = 6\) which is an integer.
- This means HCF is indeed a factor of LCM, confirming Assertion (A) is true.
Step 7: Understand how Reason (R) explains the Assertion
- Reason (R) states that the HCF divides both numbers, which is the fundamental property that allows the multiplication formula to hold.
- Because the HCF divides both \(a\) and \(b\), it also divides their LCM via the relationship.
- Therefore, Reason (R) correctly explains Assertion (A).
Final Answer: Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct explanation of Assertion (A) (Option A).
Assertion (A): The value of p for which the system of equations \(4x + py + 8 = 0\) and \(2x + 2y + 2 = 0\) is consistent is 4.
Reason (R): The system of equations \( a_1x + b_1y = c_1\) and \(a_2x + b_2y = c_2\) is consistent with infinitely many solutions, if \(\displaystyle \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}\).
Step 1: Write the given system of equations
\(4x + py + 8 = 0 \quad\) \( \Rightarrow \quad 4x + py = -8\)
\(2x + 2y + 2 = 0 \quad\) \( \Rightarrow \quad 2x + 2y = -2\)
Step 2: Identify coefficients
Comparing with the general form \(a_1x + b_1y = c_1\) and \(a_2x + b_2y = c_2\):
\(a_1 = 4, \quad b_1 = p, \quad c_1 = -8\)
\(a_2 = 2, \quad b_2 = 2, \quad c_2 = -2\)
Step 3: Use condition for consistent system with infinitely many solutions
The system is consistent with infinitely many solutions if:
\(\displaystyle \frac{a_1}{a_2} = \displaystyle \frac{b_1}{b_2} = \displaystyle \frac{c_1}{c_2}\)
Step 4: Calculate the ratios
\(\displaystyle \frac{a_1}{a_2} = \displaystyle \frac{4}{2} = 2\), \(\quad \displaystyle \frac{b_1}{b_2} = \displaystyle \frac{p}{2}\), \( \displaystyle \frac{c_1}{c_2} = \displaystyle \frac{-8}{-2} = 4\)
Step 5: Equate the ratios to find \(p\)
For the system to have infinitely many solutions, ratios must be equal:
\(2 = \displaystyle \frac{p}{2} = 4\)
But \(2 \neq 4\), so the system
cannot
be consistent with infinitely many solutions.
Step 6: Check if the system is consistent (has some solution)
For the system to be consistent (at least one solution), check if:
\(\displaystyle \frac{a_1}{a_2} \neq \displaystyle \frac{b_1}{b_2}\) or system is consistent if:
\(4x + py = -8 \quad\) and \( \quad 2x + 2y = -2\)
Step 7: Find \(p\) for which system is consistent
Multiply second equation by 2:
\(4x + 4y = -4\) Compare with first:
\(4x + py = -8\) For consistency, these lines should not be parallel (i.e. slopes differ), so:
\(p \neq 4\)
Conclusion:
- Assertion (A) states \(p = 4\) makes system consistent — this is
false
because \(p \neq 4\) ensures consistency.
- Reason (R) is
true
as it correctly states the condition for infinite solutions.
Therefore,
Option D
is correct: Assertion is false, but Reason is true.
Solve the following system of equations for \(x\) and \(y\): \(\displaystyle \frac{x}{2} + \frac{2y}{3} = -1 \) and \(\displaystyle x - \frac{y}{3} = 3 \)
(a) In the given figure, if PQ \(\parallel\) RS, then prove that \(\triangle\)POQ \(\sim\) \(\triangle\)SOR.
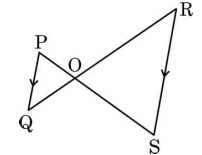
OR
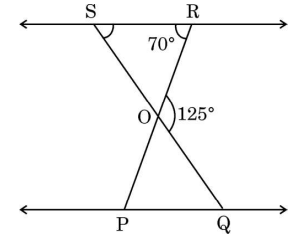
(b) In the given figure, \(\triangle\)OSR \(\sim\) \(\triangle\)OQP, \(\angle\)ROQ = 125° and \(\angle\)ORS = 70°. Find the measures of \(\angle\)OSR and \(\angle\)OQP.
Two concentric circles are of radii 6 cm and 10 cm. Find the length of the chord of the larger circle which touches the smaller circle.
(a) Find the values of A and B (\(0 \leq \text A < 90^\circ\), \(0 \leq \text B < 90^\circ\)), if \( \tan(\text A + \text B) = 1 \) and \(\displaystyle \tan(\text A - \text B) = \frac{1}{\sqrt{3}} \).
OR
(b) Prove that \( \tan 45^\circ = 1 \) geometrically.
A chord of a circle of diameter 20 cm subtends an angle of \( 60^\circ \) at the centre of the circle. Find the area of the corresponding minor segment of the circle.
(Use \( \pi = 3.14 \) and \( \sqrt{3} = 1.73 \))
(a) Prove that \( \sqrt{3} \) is an irrational number.
OR
(b) The factor tree of a number \(x\) is shown below:
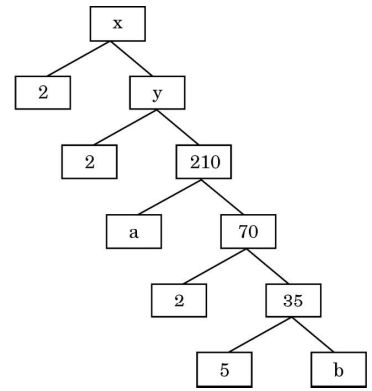
Find the values of \(x\), \(y\), \(a\), and \(b\). Hence, write the product of the prime factors of the number \(x\) so obtained.
Find a quadratic polynomial whose sum and product of zeroes are 0 and -9, respectively. Also, find the zeroes of the polynomial so obtained.
(a) Solve the following system of equations graphically: \( x + 3y = 6;\) \( 2x - 3y = 12 \)
OR
(b) \( x \) and \( y \) are complementary angles such that \( x : y = 1 : 2 \). Express the given information as a system of linear equations in two variables and hence solve it.
Prove that a rectangle circumscribing a circle is a square.
Prove that:
\(\displaystyle
\frac{1 + \cot^2 A}{1 + \tan^2 A} = \left( \frac{1 - \cot A}{1 - \tan A} \right)^2
\)
A lot consists of 200 pens of which 180 are good and the rest are defective. A customer will buy a pen if it is not defective. The shopkeeper draws a pen at random and gives it to the customer. What is the probability that the customer will not buy it?
Another lot of 100 pens containing 80 good pens is mixed with the previous lot of 200 pens. The shopkeeper now draws one pen at random from the entire lot and gives it to the customer. What is the probability that the customer will buy the pen?
(a) The difference of the squares of two positive numbers is 180. The square of the smaller number is 8 times the greater number. Find the two numbers.
OR
(b) Find the value(s) of \( k \) for which the equation \( 2x^2 + kx + 3 = 0 \) has real and equal roots. Hence, find the roots of the equations so obtained.
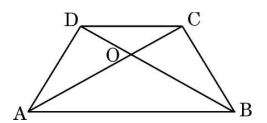
State "Basic Proportionality Theorem" and use it to prove the following:
In a quadrilateral ABCD, diagonals AC and BD intersect each other at O such that
\(\displaystyle
\frac{AO}{BO} = \frac{CO}{DO}
\)
as shown in the given figure. Prove that ABCD is a trapezium.
(a) A toy is in the form of a cone surmounted on a hemisphere. The cone and hemisphere have the same radii. The height of the conical part of the toy is equal to the diameter of its base. If the radius of the conical part is 5 cm, find the volume of the toy.
OR
(b) A cubical block is surmounted by a hemisphere of radius 3.5 cm. What is the smallest possible length of the edge of the cube so that the hemisphere can totally lie on the cube? Find the total surface area of the solid so formed.
The following data gives the information on the observed lifetime (in hours) of 200 electrical components:
| Lifetime (in hours) | Number of electrical components |
|---|---|
| 0 – 20 | 10 |
| 20 – 40 | 35 |
| 40 – 60 | 50 |
| 60 – 80 | 60 |
| 80 – 100 | 30 |
| 100 – 120 | 15 |
Find the mean lifetime (in hours) of the electrical components.
An injured bird was found on the roof of a building. The building is 15 m high. A fireman was called to rescue the bird. The fireman used an adjustable ladder to reach the roof. He placed the ladder in such a way that the ladder makes an angle of 60° with the ground in order to reach the roof.

Based on the above information, answer the following questions:
- Find the length of the ladder used by the fireman to reach the roof. 1
- Find the distance of the point on the ground at which the ladder was fixed from the bottom of the building. 1
-
In order to avoid skidding, the fireman placed the ladder in such a way that the bottom of the ladder touches the base of the wall which is opposite to the building, making an angle of 30° with the ground.
(a) Draw a neat diagram to represent the above situation and hence find the width of the road between the building and the wall. 2
OR
(b) Find the length of the ladder used by the fireman in this case. 2
In a garden, saplings of rose flowers were planted at equal intervals to form a spiral pattern. The spiral is made up of successive semicircles, with centres alternatively at A and B, starting with centre at A, of radii 50 cm, 100 cm, 150 cm, ....... as shown in the figure given below. Spiral 1 has 10 flowers, Spiral 2 has 20 flowers, Spiral 3 has 30 flowers and so on.
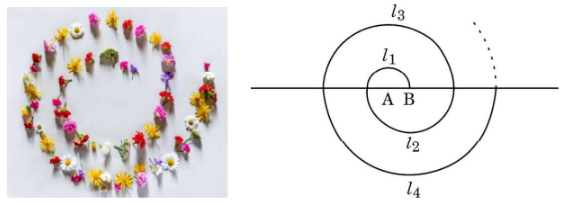
Based on the above information, answer the following questions:
- What is the radius of the 13th spiral? 1
- If the radius of the nth spiral is 500 cm, find the value of n. 1
-
(a) Find the total number of saplings till the 11th spiral. 2
OR
(b) Till which spiral, will there be a total of 450 saplings? 2
In a society, there is a circular park having two gates. The gates are placed at points A(10, 20) and B(50, 50), as shown in the figure below.
Two fountains are installed at points P and Q on AB such that AP = PQ = QB.
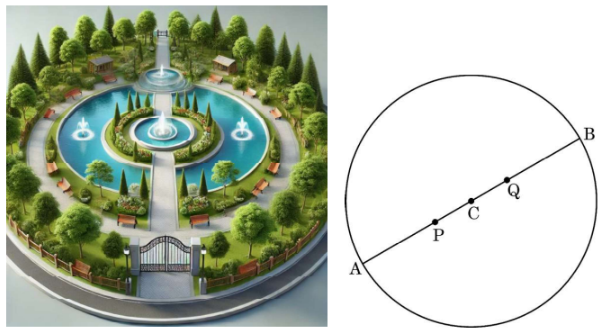
Based on the above information, answer the following questions:
- Find the coordinates of the centre C. 1
- Find the radius of the circular park. 1
-
(a) Find the coordinates of the point P. 2
OR
(b) Find the distance of the fountain at Q from gate A. 2
Download the official CBSE Class 10 Maths Basic 2025 430/1/1 Set 1
Thank You for Visiting!
Thank you for visiting thekissakahani.com – your trusted source for Previous Year Question Papers with solutions. We aim to provide well-structured practice material and detailed explanations to help students prepare effectively for their exams. Stay connected for more solved papers, exam tips, and study resources – all in one place!